Weight Correction Factor in Pulling Tension Calculations
Describes the physics behind the weight correction factor used in the pulling tension equations. Shows the weight-correction factor effect on pulling tension.
The weight correction factor
In the pulling tension equations, there is a dimensionless constant called the weight correction factor (sometimes called the occupancy factor). To understand the weight correction factor and what it implies, let’s first look at the equation for tension add-on in a straight conduit section.
| Straight Conduit Section Equation |
| Tout = Tin + WLwμ |
| Where: |
| Tout = Tension Coming Out of the Straight Section (lbf, kg, kN) |
| Tin = Tension Coming into the Straight Section (lbf, kg, kN) |
| W = Cable Weight per Unit of Length (lb, kg, kN) |
| w = Weight Correction Factor (dimensionless) |
| μ = Coefficient of Friction (COF) (dimensionless) |
This equation shows the tension add-on from a straight section is directly proportional to the weight of the cable; the section length; the friction coefficient; and the weight correction factor. As we will see, for single cable pulls, the weight correction factor (WCF) does not affect tension because it equals one (1).
| Related Content: Cable Jam Ratio Paper |
However, for pulls with more than one cable in a conduit, the WCF is a number greater than 1. How much greater? And what is the basis for weight correction factor?
The theory behind the weight correction factor
To understand the physics behind the WCF, consider the example of one versus two identical cables in a conduit.
| Figure 1. Single Cable in a Conduit |
 |
| Where: |
| D = Inner Diameter (ID) of the Conduit |
| d = Outer Diameter (OD) of the Cable |
| W = Gravitational Weight Force Vector |
| N = Normal Force Vector |
In the single cable case shown in Figure 1, the cable does not “fall” because there is a normal force (N) at the point of contact with the conduit that is equal and opposite to the gravitational weight force (W). The ratio of normal force to gravitational force is defined as the weight correction factor. In the single cable case, the weight correction factor is 1 (WCF = 1). Remember that it is the normal force multiplied by the COF that creates the frictional resistance to movement. A pulling force is required to overcome that resistance and to move the cable.
| Figure 2. Two Identical Cables in a Conduit | |
 |
 |
We see with two cables that point of contact moves up the side of the conduit. The larger the cables, the higher it moves. The normal force now comes from the vector addition of the gravitation force and a force perpendicular to the gravitational force. The normal force (the hypotenuse) is now greater than the gravitational force. The ratio of normal force to gravitational force is the weight correction factor. As the cable OD gets larger within a constant conduit ID, the normal force increases and, for two identical cables, approaches infinity as d→ D/2. However, a WCF above 2.0 is not really an issue in cable installation, because of code and cable clearance limits.
| Related Content: Coefficient of Friction in Cable Pulling — Part 1 |
Weight correction factor equations
Equations (based on D and d) can be derived for WCF. These derivations can be found in cable installation literature. The equations (for 1, 2, 3, and 4 identical cables) are:
| Weight Correction Factor Equations | ||
| |
1 Cable | |
| |
2 Cables |  |
| |
3 Cables (Triangular) |  |
| |
3 Cables (Cradled) |  |
| |
4 Cables (Diamond) |  |
Weight correction factor analysis
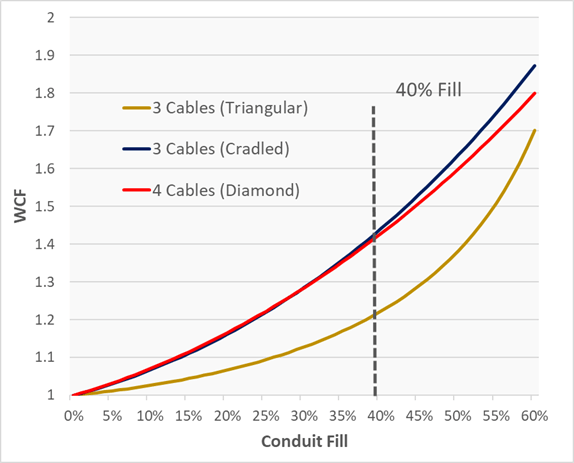
Figure 3 – WCF for various cable configurations
Figure 3 plots WCF from the three and four cable equations against conduit fill percentage. We see WCF varies from 1 to 1.4 at typical conduit fills.
Note that three cables in the cradled configuration show a higher WCF than the same three cables in the triangular configuration. In pulling calculations, it generally assumed that three cables “roll” from cradled to triangular once the center of mass of the outside cable(s) reaches a point above the base cable.
| Related Content: Coefficient of Friction in Cable Pulling Tension from Conduit Bends |
The WCF for four identical cables in the diamond configuration closely follows that of three cables cradled. This is not surprising. If we look at the geometry, we see that the contact points are similar for these configurations.
Pull-Planner™ handling of weight correction factor
The Pull-Planner software calculates the WCF for 1, 2, and 3 cables based on cable OD and conduit ID input and the equations above. For 4 or more cables, or complex configurations with cables of different sizes, the software follows the common industry approach of setting the WCF to 1.4. A WCF above 1.4 is not common in normal cable installation, so this is a conservative approach. If a “cable travel configuration” can be determined for complex multi-cable pulls, a WCF can usually be determined. While that exercise is seldom worthwhile, the Pull-Planner allows the user to override the software’s internal calculation and set a WCF when desired.
The Pull-Planner “rolls” cables from cradled to triangular at a conservative D/d <= 2.5 (48% fill). That means three-cable pulls with under 40% fill are calculated with the cradled configuration unless the cables are triplexed.
| Related Content: FAQ – Cable Pulling, Lubrication, and Tension |
The actual point where three cables might move to a triangular configuration depends not only on cable size, but also feed configuration; the existence of opposing bends causing the cables to cross the conduit; and the distribution of pulling force on the cables. If a triangular configuration is assured, the user can override WCF as described above.
Implications of weight correction factor in pulling tension calculations
We showed that the WCF in a straight-section calculation is linear. It thus typically adds 20% to 40% additional tension for multiple-cable pulls. That would, of course, be in addition to the higher cable bundle weight (two or three cables versus one).
But what about conduit bends?
| Conduit Bend Equation (simplified*) |
| Tout = Tin * ewμϴ |
| Where: |
| Tout = Tension Coming Out of the Bend (lbf, kg, kN) |
| Tin = Tension Coming into the Bned (lbf, kg, kN) |
| w = Weight Correction Factor (dimensionless) |
| μ = Coefficient of Friction (COF) (dimensionless) |
| ϴ = Angle of Bend (radians) |
| e = Naperian Log Base (constant) |
Note that in a conduit bend the WCF is an exponent in a multiplier. Plugging in the typical WCF range raises the tension coming out of a bend by 5% to 15%.
Theory vs reality
The analysis above is theoretical. Polywater® has done pull testing comparing single cable pulls to multiple cables pulls. The existence and magnitude of any WCF can be determined by comparing the measured tension results. Presenting that data will require another blog post, but for the curious, the correlation is pretty good. Leave WCF in your calculations!
