Factor de corrección de peso en los cálculos de tensión de tracción
Describe las características físicas con respecto al factor de corrección de peso utilizado en las ecuaciones de tensión de tracción. Muestra el efecto WCF [Factor de corrección de peso] sobre la tensión de tracción.
El factor de corrección de peso
En las ecuaciones de tensión de tracción, hay una constante adimensional llamada factor de corrección de peso (a veces llamado factor de ocupación). Para comprender el factor de corrección de peso y lo que implica, primero veamos la ecuación para el agregado de tensión en una sección de conducto recto.
| Ecuación de sección de conducto recto |
| Tout = Tin + WLwμ |
| Dónde: |
| Tout = Tensión de salida de la sección recta (lbf, kg, kN) |
| Tout = Tensión hacia la sección recta (lbf, kg, kN) |
| W = Peso del cable por unidad de longitud (lb, kg, kN) |
| w = Factor de corrección de peso (adimensional) |
| μ = coeficiente de fricción (COF) (adimensional) |
Esta ecuación muestra que el agregado de tensión de una sección recta es directamente proporcional al peso del cable; la longitud de la sección; el coeficiente de fricción; y el factor de corrección de peso. Como veremos, para las instalaciones de un solo cable, el factor de corrección de peso (WCF) no afecta la tensión porque es igual a uno (1).
| Contenido relacionado: Papel de Relación de Atasco de Cable |
No obstante, para instalaciones con más de un cable en un conducto, el WCF es un número mayor que 1. ¿Cuánto más grande? ¿Y cuál es la base del factor de corrección de peso?
La teoría con respecto al factor de corrección de peso
Para comprender las características físicas con respecto al WCF, considere el ejemplo de uno en comparación con dos cables idénticos en un conducto.
| Figura 1. Un solo cable en un conducto |
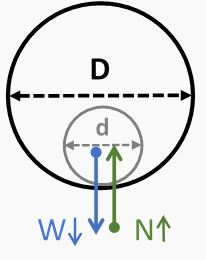 |
| Dónde: |
| D = Diámetro interior (DI) del conducto |
| d = Diámetro exterior (DE) del cable |
| W = Vector de fuerza de peso gravitacional |
| N = Vector de fuerza normal |
En el caso de un solo cable que se muestra en la Figura 1, el cable no «cae» porque hay una fuerza normal (N) en el punto de contacto con el conducto que es igual y opuesta a la fuerza de peso gravitacional (W). La relación entre la fuerza normal y la fuerza gravitacional se define como el factor de corrección de peso. En el caso de un solo cable, el factor de corrección de peso es 1 (WCF = 1). Recuerde que es la fuerza normal multiplicada por el COF lo que crea la resistencia por fricción al movimiento. Se requiere una fuerza de tracción para superar esa resistencia y mover el cable.
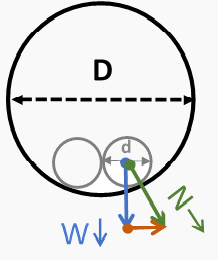
| Figura 2. Dos cables idénticos en un conducto | |
 |
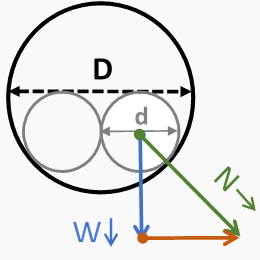 |
Vemos en el caso de los dos cables que el punto de contacto se mueve hacia arriba por el costado del conducto. Cuanto más grandes son los cables, más alto se mueve. La fuerza normal ahora proviene de la suma vectorial de la fuerza de gravitación y una fuerza perpendicular a la fuerza de gravedad. La fuerza normal (la hipotenusa) es ahora mayor que la fuerza gravitacional. La relación entre la fuerza normal y la fuerza gravitacional es el factor de corrección de peso. A medida que el diámetro exterior del cable aumenta dentro de un diámetro interior constante del conducto, la fuerza normal aumenta y, para dos cables idénticos, se acerca al infinito cuando d→ D/2. No obstante, un WCF por encima de 2.0 no es realmente un problema en la instalación de cables, debido a los límites de espacio de los cables y los códigos.
| Contenido relacionado: Coeficiente de fricción en el tirado de cables — Parte 1 |
Ecuaciones del factor de corrección de peso
Las ecuaciones (basadas en D y d) se pueden derivar para WCF. Estas derivaciones se pueden encontrar en la literatura de instalación de cables. Las ecuaciones (para 1, 2, 3 y 4 cables idénticos) son:
| Ecuaciones del factor de corrección de peso | ||
| |
1 Cable | |
| |
2 Cables | 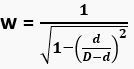 |
| |
3 Cables (Triangular) | 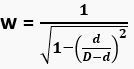 |
| |
3 cables (enrollados) | 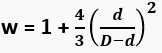 |
| |
4 Cables (Diamante) | 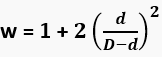 |
Análisis del factor de corrección de peso
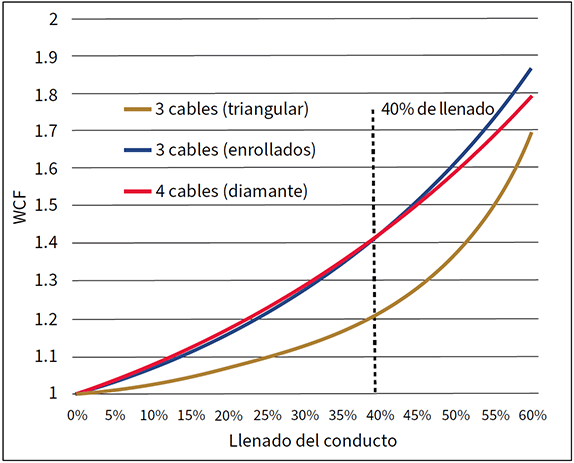
Figura 3 – WCF para varias configuraciones de cable
La Figura 3 traza el WCF de las ecuaciones de tres y cuatro cables contra el porcentaje de llenado de conductos. Vemos que el WCF varía de 1 a 1,4 en los rellenos de conductos típicos.
Observe que tres cables en la configuración acunados muestran un WCF más alto que los mismos tres cables en la configuración triangular. En los cálculos de tracción, generalmente se asumió que tres cables «se enrollan» de acunados a triangular una vez que el centro de masa de los cables externos alcanza un punto por encima del cable base.
| Contenido relacionado: Coeficiente de fricción en la tensión del tirado de cables de las curvaturas del conducto |
El WCF para cuatro cables idénticos en la configuración de diamante sigue de cerca al de tres cables acunados. Esto no sorprende. Si miramos la geometría, vemos que los puntos de contacto son similares para estas configuraciones.
Manejo de Pull-Planner™ del factor de corrección de peso
El software Pull-Planner calcula el WCF para 1, 2 y 3 cables según el diámetro exterior del cable y la entrada del ID del conducto y las ecuaciones anteriores. Para 4 o más cables, o configuraciones complejas con cables de diferentes tamaños, el software sigue el enfoque común de la industria de establecer WCF en 1.4. Un WCF por encima de 1.4 no es común en la instalación de cable normal, por lo que este es un enfoque conservador. Si se puede determinar una “configuración de recorrido del cable” para tramos complejos de múltiples cables, generalmente se puede determinar un WCF. Si bien ese ejercicio rara vez vale la pena, Pull-Planner permite al usuario anular el cálculo interno del software y establecer un WCF cuando lo desee.
El Pull-Planner «enrolla» los cables de acunados a triangulares a un conservador D/d <= 2.5 (48 % de relleno). Eso significa que las instalaciones de tres cables con menos del 40 % de relleno se calculan con la configuración acunada a menos que los cables estén triplexados.
| Contenido relacionado: Preguntas frecuentes: Tirado de cables, lubricación y tensión |
El punto real donde tres cables pueden moverse a una configuración triangular depende no solo del tamaño del cable, sino también de la configuración de la alimentación; la existencia de curvaturas opuestas que hacen que los cables crucen el conducto; y la distribución de la fuerza de tracción sobre los cables. Si se garantiza una configuración triangular, el usuario puede anular WCF como se describe anteriormente.
Implicaciones del factor de corrección de peso en los cálculos de tensión de tracción
Hemos mostrado que el WCF en un cálculo de sección recta es lineal. Por consiguiente, generalmente agrega de 20 % a 40 % de tensión adicional para instalaciones de múltiples cables. Eso, por supuesto, se sumaría al mayor peso del haz de cables (dos o tres cables frente a uno).
Pero, ¿qué sucede en cuanto a las curvaturas de los conductos?
| Ecuación de curvatura de conducto (simplificada*) |
| Tout = Tin * ewμϴ |
| Dónde: |
| Tout = Tensión de salida de la curvatura (lbf, kg, kN) |
| Tin = Tensión de entrada a la curvatura (lbf, kg, kN) |
| w = Factor de corrección de peso (adimensional) |
| μ = coeficiente de fricción (COF) (adimensional) |
| ϴ = Ángulo de curvatura (radianes) |
| e = Naperian Log Base (constante) |
Tenga en cuenta que en una curvatura de conducto el WCF es un exponente en un multiplicador. Conectar el rango WCF típico aumenta la tensión de salida de una curvatura entre un 5 % y un 15 %.
Teoría vs realidad
El análisis anterior es teórico. Polywater® ha realizado pruebas de tracción comparando instalaciones de un solo cable con instalaciones de cables múltiples. La existencia y magnitud de cualquier WCF se puede determinar comparando los resultados de tensión medidos. Presentar esos datos requerirá otra publicación de blog, pero para los curiosos, la correlación es bastante buena. ¡Deje WCF en sus cálculos!
¿Preguntas?
* La ecuación de curvatura simplificada es una aproximación que es bastante precisa cuando las tensiones entrantes son mucho mayores que el peso del cable en la curvatura.
