Gewichts-Korrekturfaktor bei der Berechnung der Zugspannung
Beschreibt die physikalischen Grundsätze des Gewichts-Korrekturfaktors, der in den Zugspannungsgleichungen verwendet wird. Zeigt die Auswirkungen des Gewichts-Korrekturfaktors auf die Zugspannung.
Gewichts-Korrekturfaktor
In den Zugspannungsgleichungen gibt es eine dimensionslose Konstante, den so genannten Gewichts-Korrekturfaktor (wird auch als Belegungsgrad oder Füllfaktor bezeichnet). Um zu verstehen, worum es sich beim Gewichts-Korrekturfaktor genau handelt, sehen wir uns zunächst die Gleichung für die zusätzliche Spannung in einem geraden Rohrabschnitt an.
| Gleichung für gerade Rohrabschnitte |
| Tout = Tin + WLwμ |
| Wobei: |
| Tout = Spannung am Ende des geraden Rohrabschnitts (kg, kN) |
| Tin = Spannung am Anfang des geraden Rohrabschnitts (kg, kN) |
| W = Kabelgewicht pro Längeneinheit (kg, kN) |
| w = Gewichts-Korrekturfaktor (dimensionslos) |
| μ = Reibungskoeffizient (dimensionslos) |
Diese Gleichung zeigt, dass die zusätzliche Spannung eines geraden Rohrabschnitts direkt proportional zum Kabelgewicht, zur Länge des Rohrabschnitts, zum Reibungskoeffizienten und zum Gewichts-Korrekturfaktor ist. Wir werden auch feststellen, dass der Gewichts-Korrekturfaktor beim Einziehen von einzelnen Kabeln keinen Einfluss auf die Spannung hat, da er gleich eins (1) ist.
| Verwandte Inhalte: Das Konzept der Verkeilung und wie es sich in einem Kabelzug auswirkt |
Werden jedoch mehrere Kabel in ein Rohr eingezogen, ist der Gewichts-Korrekturfaktor größer als 1. Um wie viel größer? Und worauf basiert der Gewichts-Korrekturfaktor?
Die theoretischen Grundsätze des Gewichts-Korrekturfaktors
Die physikalischen Grundsätze des Gewichts-Korrekturfaktor möchten wir mit einem Vergleich zwischen einem einzelnen Kabel und zwei identischen Kabeln in einem Rohr erläutern.
| Abbildung 1. Einzelnes Kabel in einem Rohr |
 |
| Wobei: |
| D = Innendurchmesser (ID) des Rohrs |
| d = Außendurchmesser (AD) des Kabels |
| W = Vektor der Schwerkraft |
| N = Vektor der Normalkraft |
Bei dem in Abbildung 1 gezeigten Beispiel mit einem Kabel „fällt“ das Kabel nicht, weil am Berührungspunkt mit dem Rohr eine Normalkraft (N) vorhanden ist, deren Größe gleich der Schwerkraft (W) ist, bei entgegengesetzter Richtung. Das Verhältnis von Normalkraft zu Schwerkraft ist als Gewichts-Korrekturfaktor definiert. Im Beispiel mit einem einzelnen Kabel beträgt der Gewichts-Korrekturfaktor 1. Denken Sie daran: Der Reibungswiderstand auf eine Bewegung ergibt sich aus der Normalkraft, die mit dem Reibungskoeffizienten multipliziert wird. Um diesen Widerstand überwinden und das Kabel bewegen zu können, ist eine Zugkraft erforderlich.
| Abbildung 2. Zwei identische Kabel in einem Rohr | |
 |
 |
Bei zwei Kabeln beobachten wir, dass der Berührungspunkt sich jetzt an der Seite des Rohrs befindet. Je größer die Kabel, desto weiter oben der Berührungspunkt. Die Normalkraft ergibt sich jetzt aus der vektoriellen Addition der Schwerkraft und einer senkrecht zur Schwerkraft wirkenden Kraft. Die Normalkraft (die Hypotenuse) ist jetzt größer als die Schwerkraft. Das Verhältnis von Normalkraft zu Schwerkraft ist der Gewichts-Korrekturfaktor. Mit zunehmendem Kabel-AD und bei gleichbleibendem Rohr-ID erhöht sich die Normalkraft und geht bei zwei identischen Kabeln mit d → D/2 gegen unendlich. Ein Gewichts-Korrekturfaktor über 2,0 stellt jedoch bei der Installation von Kabeln wegen der durch Vorschriften und Kabelabstände vorgegebenen Grenzwerte kein echtes Problem dar.
| Verwandte Inhalte: Reibungskoeffizient beim Einziehen von Kabeln – Teil 1 |
Gleichungen zum Gewichts-Korrekturfaktor
Die Gleichungen (auf der Basis von D und d) können für den Gewichts-Korrekturfaktor abgeleitet werden. Diese Ableitungen findet man in der Fachliteratur für Kabelinstallation. Die Gleichungen (für 1, 2, 3 und 4 identische Kabel) lauten:
| Gleichungen zum Gewichts-Korrekturfaktor | ||
| |
1 Kabel | |
| |
2 Kabel |  |
| |
3 Kabel (Dreieck) |  |
| |
3 Kabel (wiegenförmig) |  |
| |
4 Kabel (rautenförmig) |  |
Analyse des Gewichts-Korrekturfaktors
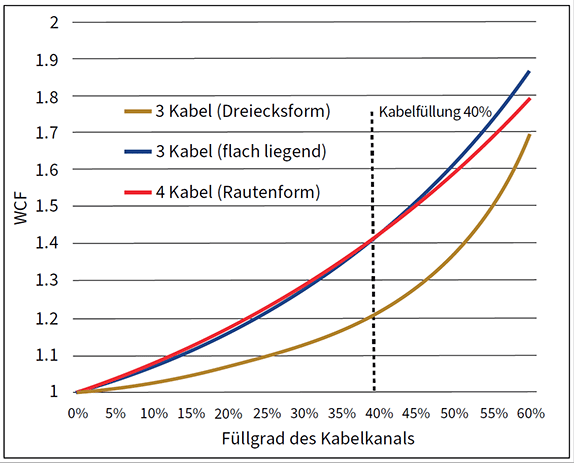
Abbildung 3 – Gewichts-Korrekturfaktor für verschiedene Kabelkonfigurationen
In Abbildung 3 wird der Gewichts-Korrekturfaktor aus den Gleichungen mit drei und vier Kabeln bei verschiedenen prozentualen Kabelfüllungen dargestellt. Der Gewichts-Korrekturfaktor bewegt sich bei typischen Kabelfüllungen zwischen 1 und 1,4.
Beachten Sie auch, dass drei Kabel in einer wiegenförmigen Anordnung einen höheren Gewichts-Korrekturfaktor aufweisen als dieselben drei Kabel in einer Dreiecksanordnung. Bei der Berechnung von Kabelzügen geht man im Allgemeinen davon aus, dass drei Kabel von der wiegenförmigen Anordnung in die Dreiecksanordnung „rollen“, wenn der Massenmittelpunkt der/des äußeren Kabel(s) einen Punkt über dem unteren Kabel erreicht.
| Verwandte Inhalte: Reibungskoeffizient beim Einziehen von Kabeln – Spannung durch Rohrkrümmungen |
Der Gewichts-Korrekturfaktor für vier identische Kabel in einer rautenförmigen Anordnung ist dem für drei Kabel ähnlich. Das überrascht uns nicht. Wenn wir uns die Geometrie ansehen, stellen wir fest, dass die Berührungspunkte für diese Anordnungen ähnlich sind.
Der Gewichts-Korrekturfaktor und Pull-Planner™
Die Pull-Planner™-Software berechnet den Gewichts-Korrekturfaktor für 1, 2 und 3 Kabel auf der Basis des Kabel-AD und des Rohr-ID sowie der oben aufgeführten Gleichungen. Bei 4 oder mehr Kabeln oder komplexen Konfigurationen mit Kabeln verschiedener Größen wendet die Software das in der Branche übliche Verfahren an und geht von einem Gewichts-Korrekturfaktor von 1,4 aus. Ein Gewichts-Korrekturfaktor über 1,4 kommt bei der Installation von normalen Kabeln nur selten vor, also handelt es sich dabei um einen vorsichtigen Ansatz. Wenn für komplexe Kabelzüge mit mehreren Kabeln eine „Kabelbewegungskonfiguration“ ermittelt werden kann, kann normalerweise auch ein Gewichts-Korrekturfaktor ermittelt werden. Das lohnt sich zwar selten, doch mit Pull-Planner kann der Anwender die interne Berechnung der Software umgehen und bei Bedarf einen Gewichts-Korrekturfaktor festlegen.
Der Pull-Planner „rollt“ Kabel mit einem vorsichtigen D/d <= 2,5 (48 % Füllung) von der wiegenförmigen in die Dreiecksanordnung. Das heißt, dass beim Einziehen von drei Kabeln mit einer Füllung unter 40 % von der wiegenförmigen Anordnung ausgegangen wird – außer es handelt sich um Triplex-Kabel.
| Verwandte Inhalte: FAQ – Einziehen von Kabeln, Schmierung und Spannung |
Der Punkt, ab dem drei Kabel in eine Dreiecksanordnung übergehen, hängt nicht nur von der Kabelgröße, sondern auch von weiteren Faktoren ab: von der Füllkonfiguration, ob entgegengesetzte Krümmungen vorhanden sind, die dazu führen, dass die Kabel das Rohr kreuzen, sowie von der Verteilung der auf die Kabel wirkenden Zugkraft. Wenn eine Dreiecksanordnung gewährleistet ist, kann der Anwender den Gewichts-Korrekturfaktor wie oben beschrieben umgehen.
Auswirkungen des Gewichts-Korrekturfaktors auf die Berechnung der Zugkraft
Wir haben gezeigt, dass der Gewichts-Korrekturfaktor bei einer Berechnung für einen geraden Rohrabschnitt linear ist. Beim Einziehen von mehreren Kabeln erhöht sich die Spannung dadurch um 20 % bis 40 %. Dies wäre natürlich zusätzlich zum höheren Gewicht des Kabelbündels (zwei oder drei Kabel anstatt einem).
Doch wie sieht es mit Rohrkrümmungen aus?
| Gleichung für Rohrkrümmungen (vereinfacht*) |
| Tout = Tin * ewμϴ |
| Wobei: |
| Tout = Spannung am Ende der Krümmung (kg, kN) |
| Tin = Spannung am Anfang der Krümmung (kg, kN) |
| w = Gewichts-Korrekturfaktor (dimensionslos) |
| μ = Reibungskoeffizient (dimensionslos) |
| ϴ = Krümmungswinkel (Bogenmaß) |
| e = Natürlicher Logarithmus (Basis e; Konstante) |
Bitte beachten Sie: Bei einer Rohrkrümmung ist der Gewichts-Korrekturfaktor ein Exponent in einem Multiplikator. Die Abdichtung im typischen Bereich des Gewichts-Korrekturfaktors erhöht die Spannung am Ende der Krümmung um 5 % bis 15 %.
Theorie und Praxis
Die oben aufgeführte Analyse ist theoretisch. Polywater® hat vergleichende Kabelzugtests mit einem Kabel und mehreren Kabeln durchgeführt. Ob ein Gewichts-Korrekturfaktor vorhanden ist, sowie dessen Größenordnung kann durch einen Vergleich der gemessenen Spannungsergebnisse ermittelt werden. Für die Vorstellung dieser Daten ist ein weiter Blog-Artikel erforderlich, doch für Wissbegierige sei vorab gesagt, dass die Korrelation ziemlich gut ist. Lassen Sie den Gewichts-Korrekturfaktor in Ihren Berechnungen bestehen!
Sie haben Fragen?
* Die vereinfachte Gleichung für Rohrkrümmungen ist eine Annäherung, die aber völlig korrekt ist, wenn die Spannungen am Anfang wesentlich höher sind als das Gewicht des Kabels in der Krümmung.
