Facteur de correction du poids dans les calculs de la tension de traction
Décrit la physique derrière le facteur de correction du poids utilisé dans les équations de tension de traction. Montre l'effet du facteur de correction du poids sur la tension de traction.
Le facteur de correction du poids
Dans les équations de tension de traction, il existe une constante sans dimension appelée facteur de correction du poids (parfois appelé facteur d’occupation). Pour comprendre le facteur de correction du poids et ce qu’il implique, examinons d’abord l’équation de l’ajout de tension dans une section de conduit droite.
| Équation de section de conduit droite |
| Tde sortie = Td’entrée + WLwμ |
| Où : |
| Tde sortie = Tension à la sortie de la section droite (lbf, kg, kN) |
| Td’entrée =Tension à l’entrée de la section droite (lbf, kg, kN) |
| W = Poids du câble par unité de longueur (lb, kg, kN) |
| w = Facteur de correction du poids (sans dimension) |
| μ = Coefficient de Friction (CDF) (sans dimension) |
Cette équation montre que l’ajout de tension d’une section droite est directement proportionnel au poids du câble, à la longueur de la section, au coefficient de friction et au facteur de correction du poids. Comme nous allons le voir, pour les tractions à câble unique, le facteur de correction du poids (FCP) n’affecte pas la tension car il est égal à un (1).
| Contenus connexes : Rapport de pourcentage de risque de blocage du câble |
Cependant, pour les tractions avec plus d’un câble dans le conduit, le FCP est un nombre supérieur à 1. Jusqu’à quel point ? Et quelle est la base du facteur de correction du poids ?
La théorie du facteur de correction du poids (FCP)
Pour comprendre la physique derrière le FCP, considérez l’exemple d’un câble unique par rapport à deux câbles identiques dans un conduit.
| Figure 1. Câble unique dans un conduit |
 |
| Où : |
| D = Diamètre intérieur (DI) du conduit |
| d = Diamètre extérieur (DE) du câble |
| W = Vecteur de la force gravitationnelle du poids |
| N = Vecteur de la force normale |
Dans le cas du câble unique illustré à la figure 1, le câble ne « tombe » pas car il existe une force normale (N) au point de contact avec le conduit qui est égale et opposée à la force gravitationnelle du poids (W). Le rapport entre la force normale et la force gravitationnelle est défini comme le facteur de correction du poids. Dans le cas d’un câble unique, le facteur de correction du poids est de 1 (FCP = 1). Rappelez-vous que c’est la force normale multipliée par le CDF qui crée la résistance de frottement au mouvement. Une force de traction est nécessaire pour surmonter cette résistance et déplacer le câble.
| Figure 2. Deux câbles identiques dans un conduit | |
 |
 |
Nous constatons avec deux câbles que le point de contact s’élève sur le côté du conduit. Plus les câbles sont gros, plus ils se déplacent en hauteur. La force normale provient maintenant de l’addition vectorielle de la force de gravitation et d’une force perpendiculaire à la force de gravitation. La force normale (l’hypoténuse) est maintenant plus grande que la force gravitationnelle. Le rapport entre la force normale et la force gravitationnelle est le facteur de correction du poids. Au fur et à mesure que le diamètre extérieur du câble s’agrandit dans un diamètre intérieur constant de conduit, la force normale augmente et, pour deux câbles identiques, s’approche de l’infini lorsque d→ D/2. Cependant, un FCP supérieur à 2,0 n’est pas vraiment un problème dans l’installation de câbles, en raison du respect du code et des limites de dégagement des câbles.
| Contenus connexes : Coefficient de friction dans le tirage de câble – Partie 1 |
Équations du facteur de correction du poids
Des équations (basées sur D et d) peuvent être dérivées pour le FCP. Ces dérivations peuvent être trouvées dans la documentation sur les installations de câbles. Les équations (pour 1, 2, 3 et 4 câbles identiques) sont les suivantes :
| Équations du facteur de correction du poids | ||
| |
1 câble | |
| |
2 câbles |  |
| |
3 câbles (en triangle) |  |
| |
3 câbles (en berceau) |  |
| |
4 câbles (en diamant) |  |
Analyse du facteur de correction du poids
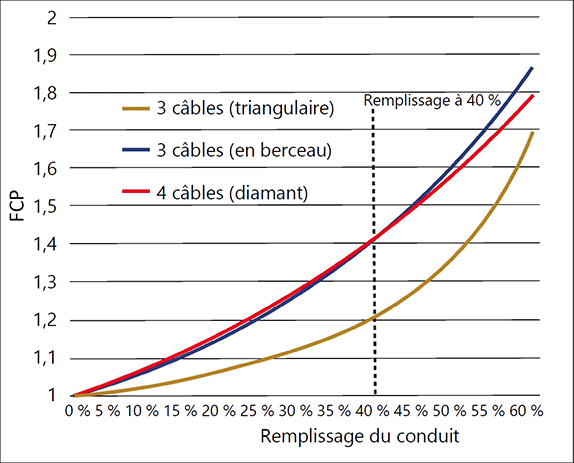
Figure 3 – FCP pour diverses configurations de câbles
La figure 3 représente le FCP des équations à trois et quatre câbles en fonction du pourcentage de remplissage du conduit. Nous constatons que le FCP varie de 1 à 1,4 pour des remplissages de conduit classiques.
Notez que trois câbles dans la configuration en berceau montrent un FCP plus élevé que les trois mêmes câbles dans la configuration en triangle. Dans les calculs de tirage, on suppose généralement que trois câbles « roulent » de l’état de berceau à celui de triangle une fois que le centre de masse du ou des câbles extérieurs atteint un point situé au-dessus du câble de base.
| Contenus connexes : Coefficient de friction dans la tension des tirages de câble due aux courbures des conduits |
Le FCP pour quatre câbles identiques dans la configuration en diamant suit de près celle de trois câbles en berceau. Cela n’est pas surprenant. Si nous examinons la géométrie, nous constatons que les points de contact sont similaires pour ces configurations.
Traitement par Pull-Planner™ du facteur de correction du poids.
Le logiciel Pull-Planner calcule le FCP pour 1, 2 et 3 câbles en se basant sur la saisie du diamètre extérieur du câble et du diamètre intérieur du conduit et sur les équations ci-dessus. Pour 4 câbles ou plus, ou pour des configurations complexes avec des câbles de tailles différentes, le logiciel suit l’approche commune du secteur qui consiste à régler le FCP sur 1,4. Un FCP supérieur à 1,4 n’est pas courant dans une installation de câble normale, il s’agit donc ici d’une approche traditionnelle. Si une « configuration de déplacement du câble » peut être déterminée pour des tractions complexes à câbles multiples, un FCP peut généralement être déterminé. Bien que cet exercice soit rarement utile, Pull-Planner permet à l’utilisateur d’ignorer le calcul interne du logiciel et de définir un FCP si nécessaire.
Le logiciel Pull-Planner « roule » les câbles d’une configuration en berceau à une configuration en triangle à une valeur conservatrice D/d <= 2,5 (48 % de remplissage). Cela signifie que les tirages à trois câbles avec un remplissage inférieur à 40 % sont calculés avec la configuration en berceau, à moins que les câbles ne soient torsadés.
| Contenus connexes : FAQ – Tirage, lubrification et tension des câbles |
Le moment où trois câbles peuvent se déplacer vers une configuration triangulaire dépend non seulement de la taille des câbles, mais aussi de la configuration de l’alimentation, de l’existence de courbes opposées amenant les câbles à traverser le conduit et de la répartition de la force de traction sur les câbles. Si une configuration en triangle est assurée, l’utilisateur peut remplacer le FCP comme décrit ci-dessus.
Implications du facteur de correction du poids dans les calculs de la tension de traction
Nous avons montré que le FCP dans un calcul de section de conduit droite est linéaire. Il ajoute donc généralement 20 à 40 % de tension supplémentaire pour les tirages à câbles multiples. Cela s’ajouterait, bien sûr, au poids plus élevé du faisceau de câbles (deux ou trois câbles comparés à un seul).
Mais qu’en est-il des courbures de conduits ?
| Équations de courbure de conduits (simplifiées*) |
| Tde sortie= Td’entrée * ewμϴ |
| Où : |
| Tde sortie = Tension à la sortie de la courbe (lbf, kg, kN) |
| Td’entrée = Tension à l’entrée de la courbe (lbf, kg, kN) |
| w = Facteur de correction du poids (sans dimension) |
| μ = Coefficient de friction (CDF) (sans dimension) |
| ϴ = Angle de courbure (radians) |
| e = Logarithme népérien (constant) |
Notez que dans une courbure de conduit, le FCP est un exposant dans un multiplicateur. L’introduction de la fourchette caractéristique de FCP augmente la tension à la sortie d’une courbe de 5 à 15 %.
Théorie vs réalité
L’analyse ci-dessus est théorique. Polywater® a effectué des tests de traction comparant les tirages de câbles simples aux tirages de câbles multiples. L’existence et l’ampleur de tout FCP peuvent être déterminées en comparant les résultats de tension mesurés. La présentation de ces données nécessitera un autre article de blog, mais pour les curieux, la corrélation est plutôt bonne. Laissez le FCP dans vos calculs !
Vous avez des questions ?
* L’équation de courbure simplifiée est une approximation qui est assez précise lorsque les tensions entrantes sont beaucoup plus importantes que le poids du câble dans la courbe.
