Model and Analysis of Duct Displacement Factor in Fiber Optic Cable Pulling—Part 2
Continued from Part 1. Because conduit is pulled from a reel when being installed underground, it’s important to recognize that there may be undulations that create low-angle bends.
In a previous article, we modeled the reel-memory displacement in continuous fiber optic duct as shown in Figure 1.
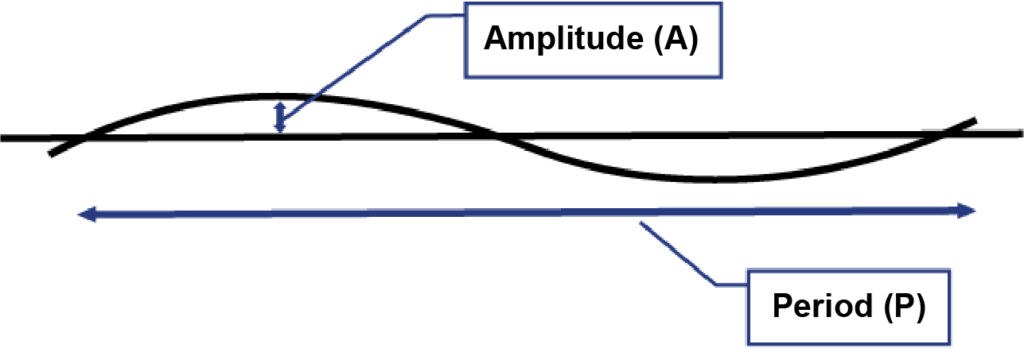
FIGURE 1. Model of Regular Duct Displacement
This model treats duct displacement as a “repeating wave” running the length of the conduit. This wave is described by its “amplitude (A)”, the maximum displacement from a straight line, and its “period (P)”, the repeating distance from peak to peak.
| Related Content: Model and Analysis of Duct Placement Factor in Fiber Optic Cable Pulling – The effect of COF on the Duct Displacement Model |
From the model, we can mathematically determine the total angle of bend per period P. The angle of bend per unit of length is more useful and can be calculated based on the repeating nature of the period. Table 1 shows a few calculations based on typical periods and amplitude data. A 12-inch amplitude might be an extreme for duct laid in an open trench and 1.5-inch typical for duct restricted inside an exterior hard-sided duct.
TABLE 1. Effective Bend Introduced by Regular Duct Displacements
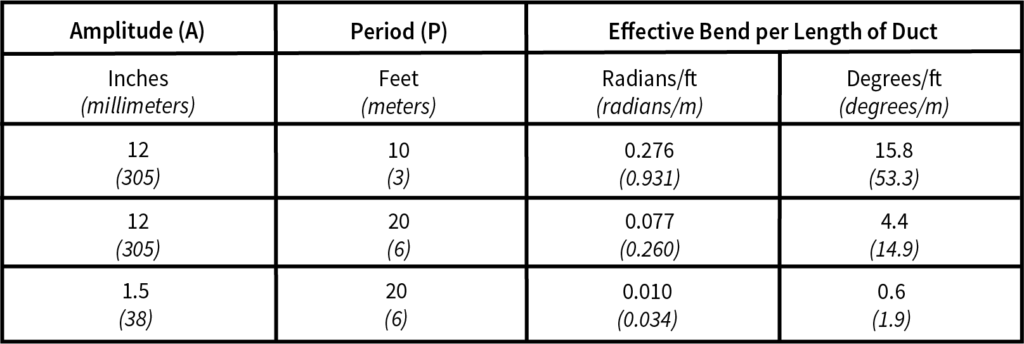
As we expect, Table 1 shows the higher the amplitude and/or the shorter the period, the higher the effective bend per unit of length. The table shows effective bends that vary from 0.6 degree/foot to as high as 15 degrees/foot of duct (2 to 50 degrees/meter). While this may not seem like much, it means hidden bend of 3,000 degrees to 75,000 degrees in 5,000 feet (1,500 m) of fiber optic pull!
| Related Content: Measuring Cable Pulling Friction with a Reel Test |
Figure 2 below graphs effective bend against displacement amplitude at three different periods. We see that even at the largest magnitude period of 30 feet, displacements of 0.5-foot (6 inches) result in greater than one degree of bend per foot. This considerable amount of bend will directly impact pull tension. The pulling equation for a bend indicates the less the bend, the lower the tension in a pull. Can we quantify this to determine allowable bend?
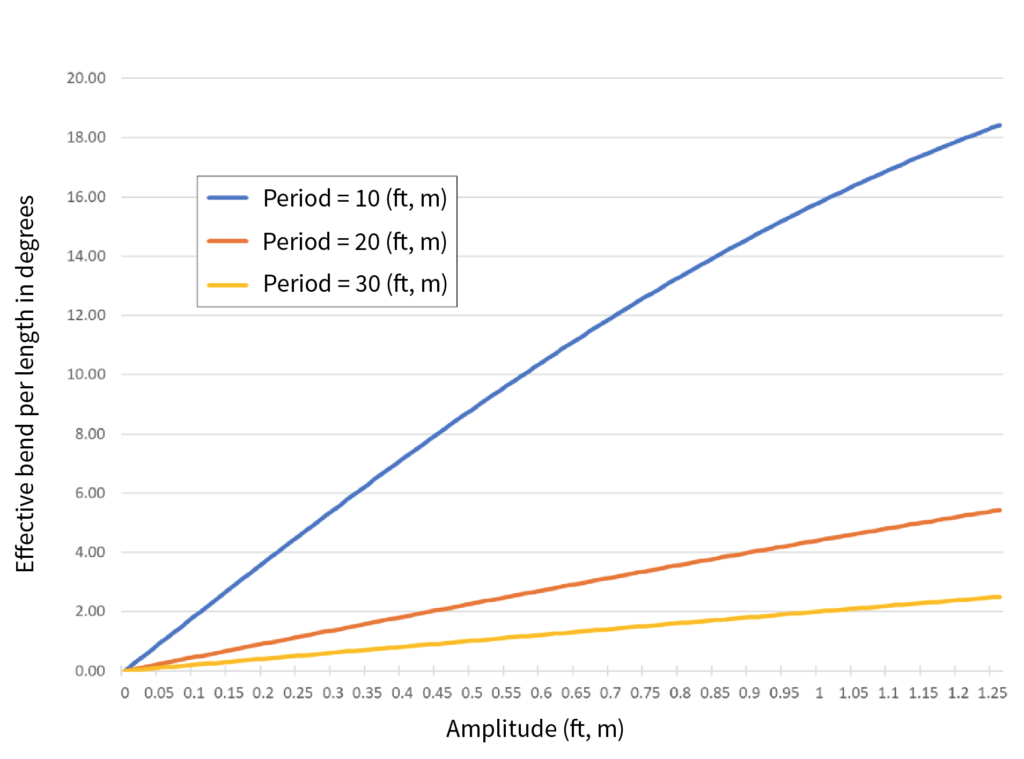
FIGURE 2. Effective Bend Resulting from Regular Duct Displacement
Pulling tension estimates using the model
To use the equations to determine tension, we must input cable weight and friction data. Figure 3 below assumes a cable weight of 0.1 lb./ft, a friction coefficient of 0.10, and an initial incoming tension on the cable of 10 lbs. It plots estimated final pulling tension against effective bend for a 1,000-, 3,000-, and 5,000-foot pull.
| Related Content: Model and Analysis of Duct Displacement Factor in Fiber Optic Cable Pulling—Part 1 |
The graph in Figure 3 shows that to keep tensions under 600 lbs. and to pull longer distances (3,000 feet plus), it is necessary to keep effective bend under 0.5 degrees per foot. This means a maximum displacement amplitude of less than 1 inch per 20-foot period.
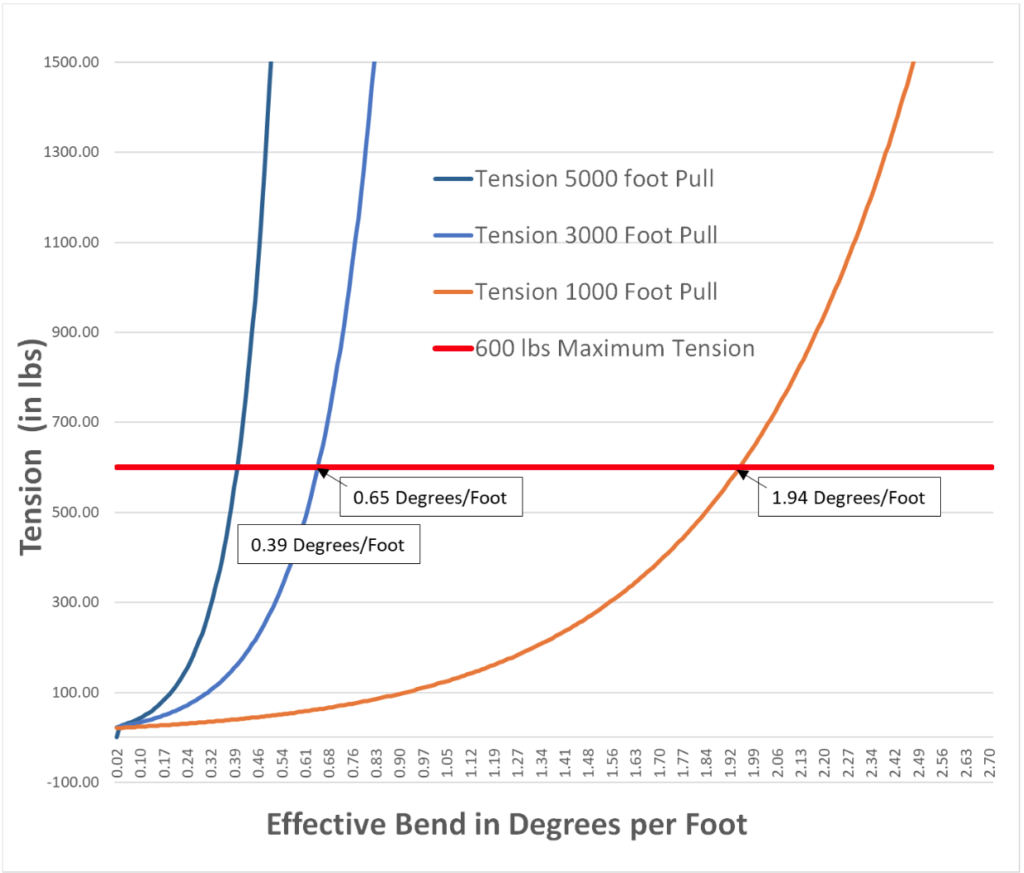
FIGURE 3. Predicted Tension vs Effective Bend
Field pulling experience
Figure 3 agrees at least anecdotally with field observations. It is usually not possible to pull cable even a thousand feet into an innerduct laid in an open trench and then covered. Even with a low COF, the pull tension exceeds 600 lbs within 1,000 feet of a pull that has 1.94 degrees of effective bend per foot. The trenched duct (A=12 inches, P=20 feet) modeled in Table 1 has twice an effective bend, 4.4 degrees/ft. But, with the lower displacements possible with pre-ripped plowing or innerduct in an outer conduit in under-bridge installations, pulls of 3,000 to 5,000 feet (1,500 m) have been done at tensions less than 600 lbs.
A potential use for this model is to use it “in reverse” to evaluate duct placement methods. Such studies have shown the importance of duct wall thickness in plowed and bored duct, the value of pre-ripping the soil in plowing, and more. Once we know the pulling tension for any given pull, we can determine the effective bend, and then experiment with the variables that may lower it.