Modelo y análisis del factor de desplazamiento de ductos en el tirado de cables de fibra óptica: Parte 2
Continuación de la parte 1. Debido a que el conducto se tira de un carrete cuando se entierra, es importante reconocer que puede haber ondulaciones que creen curvaturas de ángulo bajo.
En un artículo anterior, modelamos el desplazamiento de la memoria del carrete en un ducto de fibra óptica continuo como se muestra en la Figura 1.
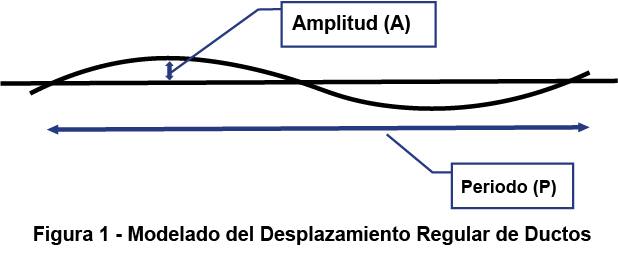
FIGURA 1. Modelo de desplazamiento de ducto regular
Este modelo trata el desplazamiento del ducto como una «onda repetitiva» que recorre la longitud del conducto. Esta onda se describe por su «amplitud (A)», el desplazamiento máximo desde una línea recta, y su «período (P)», la distancia que se repite de pico a pico.
| Contenido relacionado: Modelo y análisis del factor de desplazamiento de ductos en el tirado de cables de fibra óptica: el efecto del COF en el modelo de desplazamiento de ductos |
A partir del modelo, podemos determinar matemáticamente el ángulo total de curvatura por período P. El ángulo de curvatura por unidad de longitud es más útil y se puede calcular en función de la naturaleza repetitiva del período. La Tabla 1 muestra algunos cálculos basados en periodos típicos y datos de amplitud. Una amplitud de 12 pulgadas podría ser un extremo para un ducto colocado en una zanja abierta y una típica de 1,5 pulgadas para un ducto restringido dentro de un ducto exterior de paredes rígidas.
TABLA 1. Curvatura efectiva introducida por desplazamientos regulares de ductos
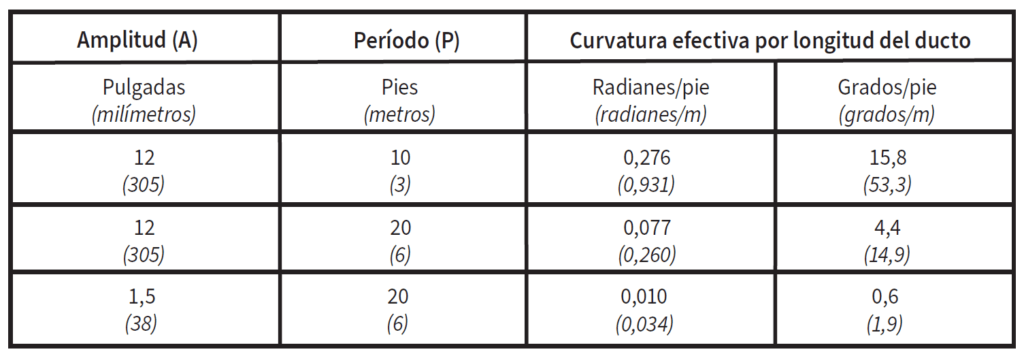
Como esperábamos, la Tabla 1 muestra que cuanto mayor sea la amplitud y/o cuanto más corto sea el período, mayor será la curvatura efectiva por unidad de longitud. La tabla muestra curvaturas efectivas que varían desde 0,6 grado/pie hasta tan alto como 15 grados/pie de ducto (2 a 50 grados/metro). Si bien esto puede no parecer mucho, ¡significa una curvatura oculta de 3.000 grados a 75.000 grados en 5.000 pies (1.500 m) de la tracción de fibra óptica!
| Contenido relacionado: Medición de la fricción de tracción del cable con una prueba de carrete |
La Figura 2 a continuación representa la flexión efectiva frente a la amplitud del desplazamiento en tres períodos diferentes. Vemos que incluso en el período de mayor magnitud de 30 pies, los desplazamientos de 0,5–pies (6 pulgadas) dan como resultado más de un grado de flexión por pie. Esta cantidad importante de curvatura afectará directamente la tensión de tracción. La ecuación de tracción para una curvatura indica que cuanto menor sea la curvatura, menor será la tensión en una tracción. ¿Podemos cuantificar esto para determinar la curvatura permitida? 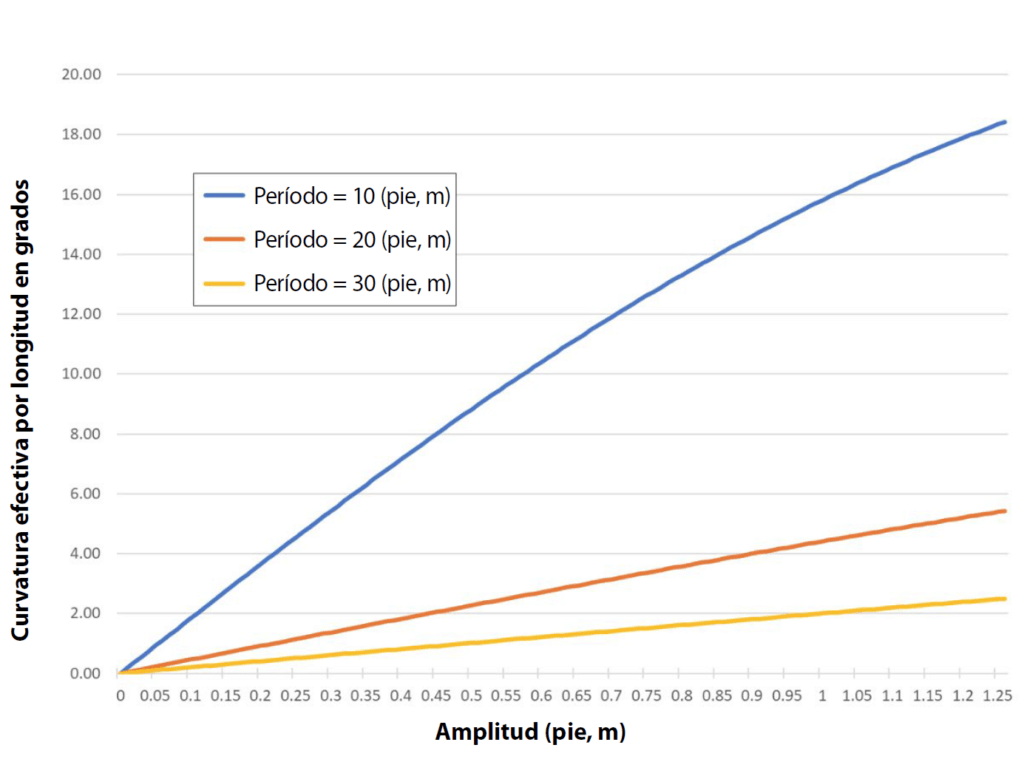
FIGURA 2. Curvatura efectiva como resultado del desplazamiento regular de ductos
Cálculos de la tensión de tracción utilizando el modelo
Para usar las ecuaciones para determinar la tensión, debemos ingresar el peso del cable y los datos de fricción. La Figura 3 a continuación asume un peso de cable de 0,1 lb/pie, un coeficiente de fricción de 0.10 y una tensión de entrada inicial en el cable de 10 lb. Se traza la tensión de tracción final estimada frente a la flexión efectiva para un tirado de 1.000, 3.000 y 5.000 pies.
| Contenido relacionado: Model and Analysis of Duct Displacement Factor in Fiber Optic Cable Pulling—Part 1 |
El gráfico en la Figura 3 muestra que para mantener las tensiones por debajo de 600 lb y para tirar distancias más largas (3.000 pies o más), es necesario mantener la flexión efectiva por debajo de 0,5 grados por pie. Esto significa una amplitud máxima de desplazamiento de menos de 1 pulgada por período de 20 pies.
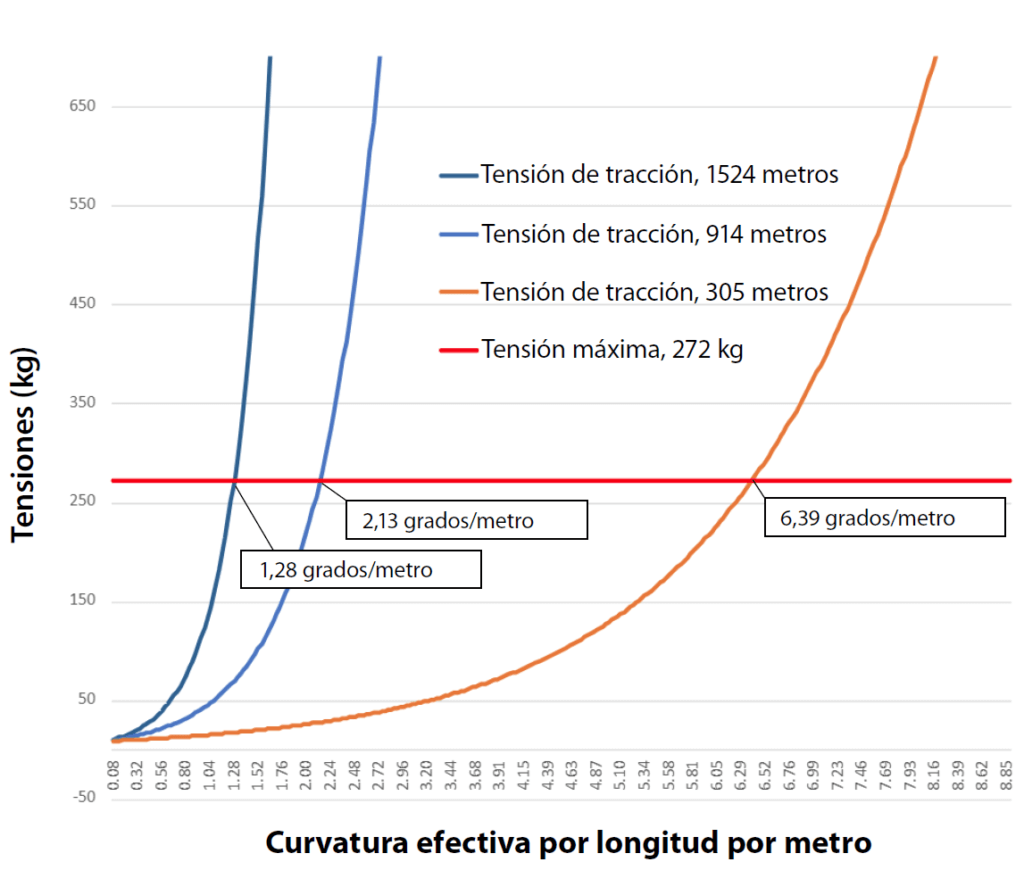
FIGURA 3 Tensión prevista frente a curvatura efectiva
Experiencia de tracción en el campo
La Figura 3 concuerda al menos anecdóticamente con las observaciones de campo. Por lo general, no es posible tirar del cable ni siquiera mil pies dentro de un conducto interior tendido en una zanja abierta y luego cubierto. Incluso con un COF más bajo, la tensión de tracción supera las 600 lb dentro de un tirado de 1.000 pies que tiene 1,94 grados de curvatura efectiva por pie. El conducto en la zanja (A=12 pulgadas, P=20 pies) que aparece en la Tabla 1 tiene el doble de curvatura efectiva, 4,4 grados/pies. Pero, con los menores desplazamientos posibles con arado precortado o conducto interno en un conducto externo en instalaciones debajo de un puente, se han realizado tiradas de 3.000 a 5.000 pies (1.500 m) con tensiones inferiores a 600 lb.
Un uso posible de este modelo es usarlo «al revés» para evaluar los métodos de colocación de ductos. Dichos estudios han demostrado la importancia del grosor de la pared del ducto en ductos arados y perforados, el valor de rasgar el suelo previamente al arar y más. Una vez que conocemos la tensión de tracción para cualquier tracción dada, podemos determinar la flexión efectiva y luego experimentar con las variables que pueden bajarla.