Modelo y análisis del factor de desplazamiento de ductos en el tirado de cables de fibra óptica: el efecto del COF en el modelo de desplazamiento de ductos
En este artículo le mostraremos cómo el coeficiente de fricción (COF) afecta la tensión del cable cuando se tira a través de las ondulaciones o desplazamientos regulares del ducto.

Se ha modelado el desplazamiento de la memoria del carrete en un ducto de fibra óptica continuo como se muestra en la Figura 1. El desplazamiento del ducto se trata como una «onda repetitiva» que recorre la longitud del conducto, con una “amplitud (A)” y un “periodo (P)”. La Parte 1 de esta serie describe la teoría detrás de este modelo. La Parte 2 de esta serie muestra cómo calculamos el ángulo introducido (por unidad de longitud) por los desplazamientos regulares. Luego, las ecuaciones de tracción se pueden usar para calcular la tensión de tracción según el ángulo total en una tirada. En esta entrega, la Parte 3 muestra cómo el coeficiente de fricción (COF) afecta la tensión del cable cuando se tira a través de estas ondulaciones o desplazamientos regulares del ducto.
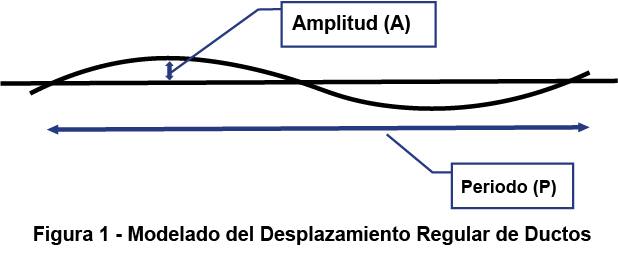
FIGURA 1. Modelo de desplazamiento de ducto regular
Las publicaciones anteriores muestran el efecto de las variaciones de amplitud y periodo en un ángulo de curvatura y tensión de tracción. El análisis muestra que, para hacer tiradas largas de cable de fibra óptica (miles de pies) a tensiones de tracción seguras, la curvatura de desplazamiento se debe mantener muy por debajo de los 1.6 grados por metro (0.5 grados por pie).
| Contenido relacionado: Modelo y análisis del factor de desplazamiento de ductos en el tirado de cables de fibra óptica: Parte 1 |
El efecto de la fricción en el modelo
Sabemos que la fricción, medida como “coeficiente de fricción”, es una variable importante con respecto a la tensión de tracción. En una sección recta del conducto, la tensión de tracción es directamente proporcional al COF. Entonces, si duplicamos el COF, duplicamos la tensión durante una tirada. En cambio, si reducimos el COF a la mitad, podemos tirar el doble de distancia con la misma tensión.
¿Qué es lo que sucede con los cambios de fricción en el enfoque de desplazamiento continuo de este modelo?
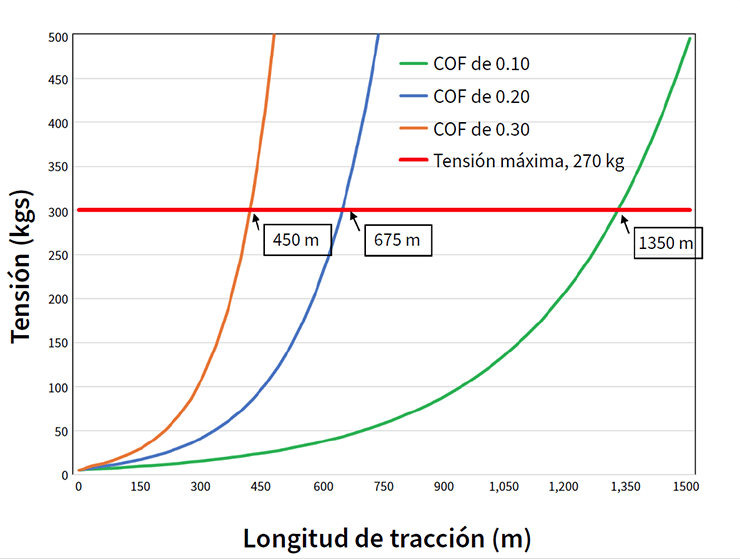
FIGURA 2. Tensión vs. longitud de tracción (ángulo de desplazamiento = 0.5°/pie)
La Figura 2 ilustra la tensión vs. la distancia para una tirada de cable de fibra de óptica. El ángulo de desplazamiento se estableció en 1.6 grados por metro (0.5 grados por pie). Los cálculos usan un peso del cable de 150 gm/m (0.1 lb-pie) y una tensión entrante inicial de 45 N (10 lb). Se calcularon tres coeficientes de fricción (COF = 0.10, COF = 0.20 y COF = 0.30) que representan un rango de fricción típico según medidas en el campo y en laboratorio.
El gráfico muestra la importancia de minimizar la fricción. Puede hacer una tirada tres veces más lejos con la misma tensión cuando se reduce el COF por un factor de tres. La distancia que se puede tirar de un cable con una tensión determinada es inversamente proporcional al coeficiente de fricción, al igual que en el cálculo de una sección recta. En el gráfico se calculan 600 lb de tensión a 4400 pies, 2200 pies y 14 pies con los coeficientes de fricción de 0.10, 0.20 y 0.30, respectivamente.
| Contenido relacionado: Cómo evitar aplastar el cable de fibra óptica durante la instalación |
La teoría
Esta linealidad sorprende un poco cuando observamos la fórmula simplificada (un cálculo*) de la ecuación de tracción de flexión (Ecuación 1). La fricción está en un exponente, que no implicaría típicamente que haya linealidad.
Curvatura del conducto Tout = Tin eμϴ
Dónde:
Tout = Tensión de salida
Tin = Tensión de entrada
μ = Coeficiente de fricción
ϴ = Ángulo de curvatura (radianes)
e = Base de logaritmo neperiano
No obstante, si observamos más de cerca, notamos que, cuando la “Tensión de salida” y la “Tensión de entrada” son constantes, el factor eμϴ también debe permanecer constante. Los cambios en μ (COF) se deben compensar con cambios recíprocos en ϴ. En otras palabras, los ángulos de curvatura más grandes se pueden compensar con un COF más bajo.
Sin embargo, ϴ es el ángulo de curvatura total, que podemos describir de la siguiente manera:
ϴ = φ * d (Ecuación 2)
Dónde:
ϴ = Ángulo total de curvatura
φ = Ángulo de desplazamiento por longitud (0.5 grados/pie en la Figura 2)
d = Distancia de tirado o longitud total.
Entonces, si duplicamos μ, se debe reducir la distancia a la mitad para reducir el ángulo total por el factor de 2. La proporcionalidad inversa resulta de la construcción de la curvatura total proporcional a la distancia en el modelo.
En publicaciones anteriores se demostró que el ángulo de desplazamiento del ducto puede variar en un orden de magnitud según el método de desplazamiento del ducto (de 0.2° a 2.0°). La Ecuación 1 refuerza la importancia de minimizar el ángulo de desplazamiento. Simplemente no es posible compensar el efecto de mayores desplazamientos con menor fricción.
| Contenido relacionado: Los orígenes de la lubricación en el soplado de cables: Una entrevista con el experto Willem Griffioen |
Tensión entrante
Por último, la Ecuación 1 muestra la importancia de una tensión entrante mínima. Si la tensión entrante se duplica, notamos que la tensión se duplica. La distancia de tirado con una tensión determinada también se reduce notablemente.
Calculadora disponible
Si le interesa obtener la calculadora (Excel) que se utilizó en este análisis, complete el formulario “Envíenos un correo electrónico” que aparece a continuación. Uno de nuestros técnicos le enviará la calculadora y se pondrá en contacto con usted para explicarle los detalles de la introducción de datos.
*El cálculo en la Ecuación 1 es bastante preciso cuando las tensiones entrantes son mucho mayores que el peso del cable en la curvatura. Sin embargo, en cuanto a las curvaturas de radio predichas según el modelo de desplazamiento, se usaron las ecuaciones completas (que incluyen un componente de peso) en los cálculos de los gráficos. Esas ecuaciones predicen una mayor tensión que el cálculo, en especial cuando la tensión entrante se acerca a cero.