Modèle et analyse du facteur de placement des conduits dans le tirage de câbles à fibre optique – L’effet du CDF sur le modèle des déplacements du conduit
Dans cet article, nous montrons comment le coefficient de friction (CDF) influe sur la tension du câble lorsque celui-ci passe par des ondulations ou des déplacements réguliers du conduit lors du tirage.

Le déplacement occasionné par la mémoire des bobines dans un conduit de fibre optique continu a été modélisé et représenté à la figure 1. Ce déplacement du conduit est traité comme une « onde répétitive » courant sur toute la longueur du conduit, que l’on peut caractériser par une « amplitude (A) » et une « période (P) ». La Partie 1 de cette série décrit la théorie qui sous-tend ce modèle. La Partie 2 de cette série montre comment on peut calculer l’angle introduit (par unité de longueur) par les déplacements réguliers. Les équations de traction peuvent ensuite être utilisées pour estimer la tension de traction en fonction de l’angle total d’un tirage. Dans la partie 3 de cette série, nous montrons comment le coefficient de friction (CDF) influe sur la tension du câble lorsque celui-ci passe par des ondulations ou des déplacements réguliers du conduit lors du tirage.
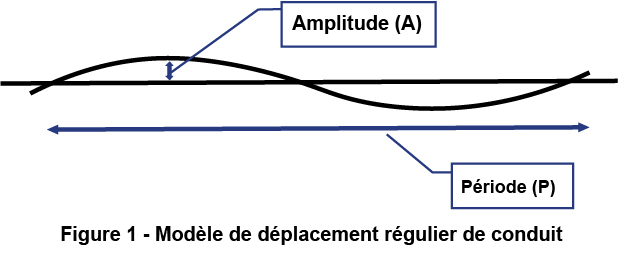
Les articles précédents ont montré l’effet des variations d’amplitude et de période sur l’angle de courbure et la tension de traction. L’analyse montre que, pour réaliser des tirages de fibres sur de grandes longueurs (sur des milliers de mètres) à des tensions de traction ne posant pas de problèmes, la courbure du déplacement doit rester bien en dessous de 1,6° par mètre.
| Contenu connexe : Modèle et analyse du facteur de déplacement du conduit dans le tirage de câble à fibre optique – Partie 1 |
L’effet de la friction sur le modèle
Nous savons que la friction, que l’on mesure grâce au « coefficient de friction » (CDF), est une variable importante de la tension de traction. Dans une section de conduit droite, la tension de traction est directement proportionnelle au CDF. Si on double le CDF, on double donc la tension lors d’un tirage. À l’inverse, si on divise par deux le CDF, on peut tirer sur une longueur deux fois plus grande avec la même tension.
Qu’en est-il des changements de friction dans l’approche de ce modèle qui s’intéresse à des déplacements continus ?
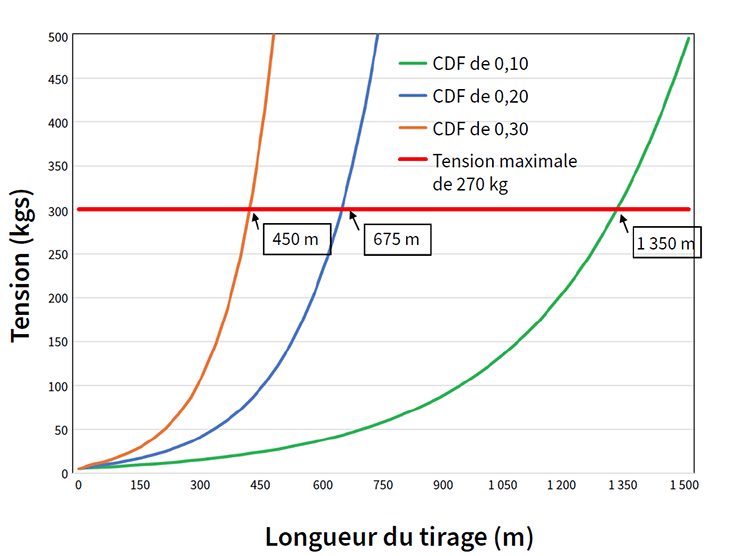
FIGURE 2. Tension en fonction de la longueur du tirage (angle du déplacement = 0,5°/pied)
La figure 2 représente la tension en fonction de la distance pour un tirage de fibre optique. L’angle de déplacement a été fixé à 1,6° par mètre. Les calculs utilisent un poids de câble de 150 g/m et une tension d’entrée initiale de 45 N. Trois coefficients de friction sont calculés (CDF = 0,10, CDF = 0,20 et CDF = 0,30), ce qui représente une plage de friction type sur la base des mesures relevées sur le terrain et en laboratoire.
Le graphique montre l’importance que revêt la minimisation de la friction. Lorsque le CDF est réduit d’un facteur trois, on peut tirer un câble sur une longueur trois fois plus grande avec la même tension. La distance sur laquelle un câble peut être tiré pour une tension donnée est inversement proportionnelle au coefficient de friction, tout comme dans le calcul effectué pour une section droite. Le graphique estime une tension de 600 lb pour un tirage de 4 400 pieds, 2 200 pieds et 14 pieds avec des coefficients de friction de 0,10, 0,20 et 0,30, respectivement.
| Contenu connexe : Comment éviter d’écraser un câble à fibre optique pendant l’installation |
La théorie
Cette linéarité est légèrement surprenante lorsque l’on observe la forme simplifiée (qui constitue une approximation*) de l’équation de traction dans un coude (équation 1). La friction est en exposant, ce qui ne se traduit normalement pas par une linéarité.
Courbure du conduit Tsortie = Tentrée eμϴ
Où :
Tsortie = Tension de sortie
Tentrée = Tension d’entrée
μ = Coefficient de friction
ϴ = Angle de courbure (en radians)
e = Logarithme népérien
Cependant, en y regardant de plus près, on constate que lorsque la « Tension de sortie » et la « Tension d’entrée » sont constantes, le facteur eμϴ doit également rester constant. Les changements de μ (le CDF) doivent être compensés par des changements réciproques de ϴ. En d’autres termes, des angles de courbure plus importants peuvent être compensés par un CDF plus faible.
Mais ϴ est l’angle total de courbure, que l’on peut décrire comme suit :
ϴ = φ x d (équation 2)
Où :
ϴ = Angle total de courbure
φ = Angle de déplacement par unité de longueur (0,5°/pied dans la figure 2)
d = Distance de traction ou longueur totale.
Ainsi, si nous doublons μ, la distance doit être divisée par deux pour réduire l’angle total d’un facteur 2. Cette proportionnalité inverse résulte du fait que la courbure totale croît proportionnellement à la distance dans le modèle.
Les articles précédents ont montré que l’angle de déplacement du conduit pouvait varier d’un facteur 10 en fonction de la méthode de placement des conduits (de 0,2° à 2,0°). L’équation 1 prouve l’importance de réduire au maximum l’angle de déplacement. En effet, il n’est tout simplement pas possible de compenser l’effet de déplacements trop importants par une réduction des frottements.
| Contenu connexe : Les origines de la lubrification dans le soufflage de câble : Un entretien avec l’expert Willem Griffioen |
Tension entrante
Enfin, l’équation 1 montre l’importance d’une tension entrante la plus basse possible. Si la tension entrante double, on constate que la tension double. La distance du tirage à une tension donnée est également réduite de manière significative.
Calculatrice disponible
Si vous êtes intéressé par la calculatrice (Excel) que nous avons utilisée dans cette analyse, veuillez remplir le formulaire « Envoyez-Nous un E-mail » ci-dessous. L’un de nos techniciens vous enverra la calculatrice et vous contactera pour vous expliquer en détail comment saisir les données.
* L’approximation que représente l’équation 1 est assez fiable lorsque les tensions entrantes sont beaucoup plus importantes que le poids du câble dans le coude. Cependant, pour les courbures à rayon élevé qui ont été prédites par le modèle de déplacement, c’est l’équation complète (qui intègre une composante de poids) qui a été utilisée pour réaliser les calculs représentés sur les graphiques. Ces équations prédisent une tension plus élevée que dans le cas de l’approximation, en particulier lorsque la tension entrante s’approche de zéro.