Modello e analisi del fattore di posizionamento del condotto nella trazione del cavo in fibra ottica – L’effetto del COF sul modello di spostamento del condotto
In questo articolo, mostriamo come il coefficiente di attrito (COF) influisce sulla tensione del cavo quando viene tirato durante le ondulazioni del condotto o i regolari spostamenti.

Lo spostamento dovuto alla memoria della bobina nel condotto in fibra ottica continua è stato modellato come mostrato nella Figura 1. Lo spostamento del condotto viene trattato come “onda ripetuta” che si estende lungo l’intera lunghezza del condotto, con “ampiezza (A)” e “periodo (P)”. La parte 1 di questa serie descrive la teoria alla base di questo modello. La parte 2 di questa serie mostra come possiamo calcolare l’angolo introdotto (per unità di lunghezza) dagli spostamenti regolari. Quindi, le equazioni di trazione possono essere utilizzate per stimare la tensione di trazione in base all’angolo totale in una trazione. In questa fase, la parte 3 illustra come il coefficiente di attrito (COF) influisce sulla tensione del cavo quando viene tirato durante queste ondulazioni o regolari spostamenti del condotto.
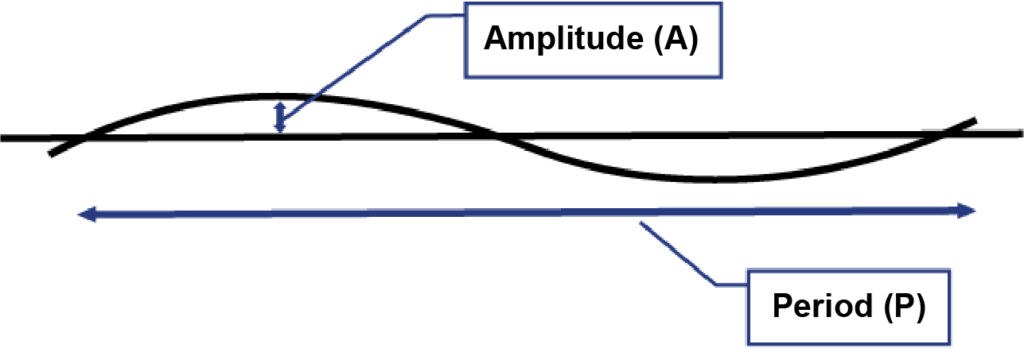
FIGURA 1. Modello di spostamento regolare del condotto
I post precedenti hanno mostrato l’effetto delle variazioni di ampiezza e periodo sull’angolo di curvatura e sulla tensione di trazione. L’analisi dimostra che, per effettuare lunghe trazioni di fibre (migliaia di piedi) a tensioni di trazione sicure, la curvatura di spostamento deve essere mantenuta ben al di sotto di 0,5 gradi per piede (1,6 gradi per metro).
| Contenuti connessi: Modello e analisi del fattore di spostamento del condotto nella trazione del cavo in fibra ottica – Parte 1 |
L’effetto dell’attrito nel modello
Sappiamo che l’attrito, misurato come “coefficiente di attrito” (COF), è una variabile importante nella trazione. In un tratto rettilineo di condotta, la tensione di trazione è direttamente proporzionale al COF. Quindi, se raddoppiamo il COF, raddoppiamo la tensione in trazione. Al contrario, se dimezziamo il COF, possiamo tirare il doppio della distanza con la stessa tensione.
Cosa succede con le variazioni di attrito nell’approccio con spostamento continuo in questo modello?
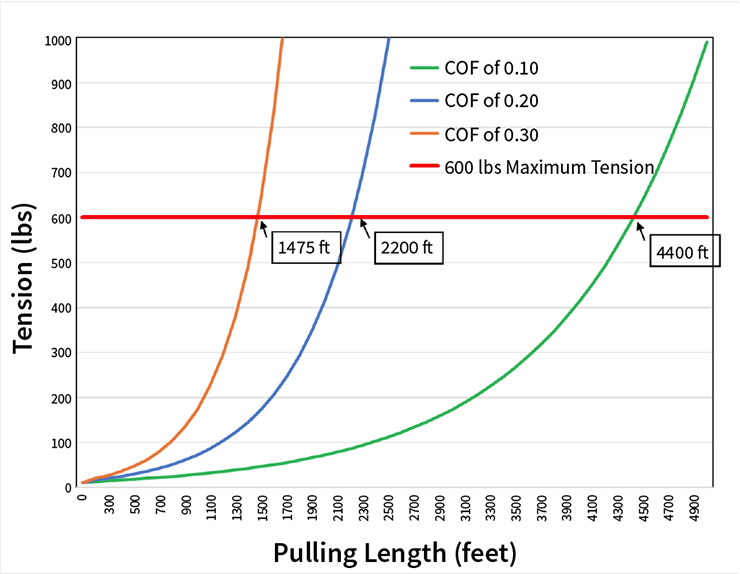
FIGURA 2. Tensione vs lunghezza di trazione (angolo di spostamento = 0,5°/ft)
La figura 2 illustra graficamente la tensione in funzione della distanza per una trazione di fibra ottica. L’angolo di spostamento è stato impostato su 0,5 gradi per piede (1,6 gradi per metro). I calcoli utilizzano un peso del cavo pari a 0,1 lb/ft. (150 g/m) e una tensione iniziale in entrata di 10 lb. (45 N). Vengono calcolati tre coefficienti di attrito (COF = 0,10, COF = 0,20 e COF = 0,30), che rappresentano un intervallo di attrito tipico basato su misurazioni effettuate sul campo e in laboratorio.
Il grafico mostra l’importanza di ridurre al minimo l’attrito. È possibile tirare tre volte più lontano con la stessa tensione riducendo il COF di un fattore tre. La distanza alla quale un cavo può essere tirato con una data tensione è inversamente proporzionale al coefficiente di attrito, proprio come nel calcolo di una sezione rettilinea. Il grafico stima una tensione di 600 libbre a 4400 piedi, 2200 piedi e 14 piedi con coefficienti di attrito rispettivamente di 0,10, 0,20 e 0,30.
| Contenuti connessi: Come evitare di schiacciare il cavo in fibra durante l’installazione |
La teoria
Questa linearità è un po’ sorprendente se consideriamo la forma semplificata (un’approssimazione*) dell’equazione di trazione in curva (equazione 1). L’attrito è in un esponente, il che in genere non implicherebbe linearità.
Curva del condotto Tout = Tin eμϴ
Dove:
Tout = Tensione esterno
TIn = Tensione interno
μ = Coefficiente di attrito
ϴ = Angolo di curvatura (radianti)
e = Base del logaritmo naperiano
Tuttavia, a un esame più attento, vediamo che quando “Tensione esterno” e “Tensione interno” sono costanti, anche il fattore eμϴ deve rimanere costante. Le variazioni di μ (COF) devono essere compensate con le variazioni reciproche di ϴ. In altre parole, angoli di curvatura più elevati possono essere compensati da un COF più basso.
Ma ϴ è l’angolo di curvatura totale, che possiamo descrivere come:
ϴ = φ * d (Equazione 2)
Dove:
ϴ = Angolo di curvatura totale
φ = Angolo di spostamento per lunghezza (0,5 gradi/piede nella Figura 2)
d = Distanza di trazione o lunghezza totale.
Quindi, se raddoppiamo μ, la distanza deve essere dimezzata per ridurre l’angolo totale di un fattore 2. La proporzionalità inversa risulta dalla curvatura totale che aumenta proporzionalmente alla distanza nel modello.
I post precedenti hanno mostrato che l’angolo di spostamento del condotto può variare di un ordine di grandezza in base al metodo di posizionamento del condotto (da 0,2° a 2,0°). L’equazione 1 rafforza l’importanza di minimizzare l’angolo di spostamento. Semplicemente non è possibile compensare l’effetto di spostamenti maggiori con un attrito ridotto.
| Contenuti connessi: Le origini della lubrificazione nel soffiaggio dei cavi: Un’intervista con l’esperto Willem Griffioen |
Tensione in ingresso
Infine, l’equazione 1 mostra l’importanza della minima tensione in ingresso. Se la tensione in ingresso raddoppia, vediamo che la tensione raddoppia. Anche la distanza di trazione con una tensione data si riduce notevolmente.
Calcolatore disponibile
Se desideri ottenere il calcolatore (Excel) utilizzato in questa analisi, compila il modulo “Mandaci un’e-mail” qui sotto. Uno dei nostri tecnici ti invierà il calcolatore e ti contatterà per spiegarti i dettagli dell’inserimento dei dati.
*L’approssimazione nell’equazione 1 è piuttosto accurata quando le tensioni in entrata sono molto maggiori del peso del cavo nella curva. Tuttavia, per le curve a raggio ampio previste dal modello di spostamento, per i calcoli del grafico è stata utilizzata l’equazione completa (che include una componente di peso). Tali equazioni prevedono una tensione maggiore rispetto all’approssimazione, soprattutto quando la tensione in ingresso si avvicina allo zero.