Modèle et analyse du facteur de déplacement des conduits dans le tirage de câbles à fibre optique – Partie 1
Comme le conduit est tiré d'une bobine lorsqu'il est enfoui sous terre, il est important de savoir qu'il peut y avoir des ondulations qui créent des courbes à angle faible.
Pourquoi le déplacement des conduits est-il important pour l’installation souterraine de la fibre ?
Comme le conduit est tiré d’une bobine lorsqu’il est enfoui sous terre, il est important de savoir qu’il peut y avoir des ondulations qui créent des courbes à angle faible. Durant l’installation, le conduit peut donner l’impression d’être droit, mais lorsque l’on tire un câble sur de longues distances, ces légères courbures dans le conduit peuvent s’additionner et produire des tensions de tirage plus élevées.
| Contenus connexes : Modèle et analyse du facteur de déplacement de la gaine dans le tirage de câble à fibre optique – Partie 2 |
Qu’est-ce qui est différent dans le tirage de câbles à fibre optique ?
Lors d’un tirage de câble à fibre optique souterrain, on souhaite souvent obtenir une portée de câble ininterrompue aussi longue que possible. Ainsi, si le câble est livré sur une bobine de 10 km (32 800 pi), nous voulons une portée complète et ininterrompue de 10 km pour éliminer toute atténuation due à une épissure.
Pour déterminer les longueurs de tirage possibles, nous pouvons utiliser les « équations de tirage de câble » pour estimer la tension de tirage du câble en fonction de la friction, du poids du câble et des détails du parcours du conduit. Ces estimations ont montré une bonne corrélation avec la tension mesurée sur le terrain lorsque des câbles lourds sont tirés dans un conduit à parois rigides, mais la longueur des parcours est beaucoup plus courte que ce que nous voulons pour la fibre. De plus, un câble à fibre optique est beaucoup plus léger qu’un câble en cuivre à paire torsadée.
Les équations prédisent que la fibre peut être tirée sur des distances beaucoup plus longues que ce qui est possible aujourd’hui. En supposant une tension maximale typique de 2,7 kN (600 lb), la théorie dit qu’il devrait être possible de tirer un câble en fibre (avec un poids normal de 150 kg/km [100 livres/1 000 pieds]) sur plus de 9 km (30 000 pieds). Cette estimation utilise un coefficient de friction de 0,2, et ce n’est pas déraisonnable car des coefficients de friction beaucoup plus bas ont été mesurés en utilisant les lubrifiants de tirage de fibre optique haute performance de Polywater.
L’expérience réelle sur le terrain montre que des distances de tirage plus typiques de 0,46 à 0,61 km (1 500 à 2 000 pieds) permettent de maintenir des tensions inférieures à 2,7 kN (600 lb), même dans un système de conduits neufs et bien positionnés. Pourquoi les tirages de câble à fibre optique présentent-ils une corrélation aussi faible avec les calculs basés sur la théorie ?
| Contenus connexes : Mesurer la friction de tirage de câble à l’aide d’un test avec dévidoir |
Le facteur conduit
Le câble à fibre optique est généralement tiré dans un conduit continu, enroulé, en PE ou en PVC flexible. Lorsque ce conduit est déroulé de la bobine et qu’il est tiré, posé dans des tranchées ou installé par système de labourage ou de forage, il conserve une certaine mémoire de la bobine qui produit des ondulations ou des déplacements légers, mais réguliers. Alors qu’un parcours semble « rectiligne », les déplacements de la mémoire de la bobine du conduit se comportent comme des coudes à angle faible. Avec les longs tirages typiques de la fibre optique, ces courbures s’additionnent et produisent une tension plus élevée que prévu.

Pour mieux comprendre, examinons la forme simplifiée de l’équation de la courbure d’un tirage de câble.
Courbure du conduit Tout = Tin eμϴ
Où :
Tout = Tension de sortie
Tin = Tension d’entrée
e = Logarithme népérien
μ = Coefficient de friction
ϴ = Angle de courbure (radians) )
Nous voyons que si nous doublons l’angle de courbure, le multiplicateur s’élève au carré, et l’angle augmente dix fois le multiplicateur à la puissance dix. L’angle est en exposant.
| Contenus connexes : La planification des projets de câblage améliore la réussite et la sécurité |
Facteur de modélisation des conduits.
Pour quantifier ce phénomène dans le tirage des fibres optiques, nous devons modéliser le déplacement du conduit, comme le montre la figure 1.
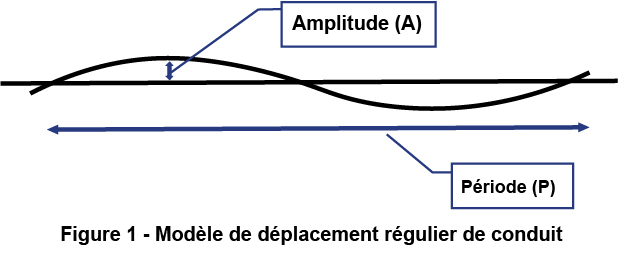
Ce modèle traite le déplacement comme une « onde répétitive » sur toute la longueur du conduit. Cette onde est décrite par son « amplitude (A) », le déplacement maximal par rapport à une ligne droite, et sa « période (P) », la distance répétée d’un pic à l’autre. On peut supposer que P est lié au diamètre de la bobine du conduit et A à la méthode d’installation du conduit.
Les placements sur le terrain ont montré que plusieurs variables affectent l’amplitude et la période. Il s’agit notamment du type de conduit, de l’épaisseur de la paroi, du diamètre de la bobine, du diamètre extérieur du conduit et de la méthode de placement. Dans le cas d’un conduit interne enroulé sur bobine et placé dans une tranchée ouverte, une onde d’une amplitude de 12 pouces (300 mm) et d’une période de répétition de 20 pieds (3 m) a été observée. Le même conduit tiré dans un tube PVC Schedule 80 de 100 mm (4 po) pourrait n’avoir qu’une amplitude de 20 mm (0,75 po) tous les 3 m (20 pi). Pour les conduits à paroi épaisse utilisés pour le « labourage » et le forage directionnel, les déplacements réguliers ne sont pas facilement observables mais on sait qu’ils dépendent du type de sol et de la roche, et ils peuvent être mesurés à l’aide de robots de géolocalisation passant dans le conduit.
| Contenus connexes : Coefficient de friction dans la tension des tirages de câble due aux courbures des conduits |
Ce modèle nous permet de quantifier la « courbure » dans un parcours « droit » en fonction de l’amplitude du déplacement et de la période de répétition, puis d’utiliser les équations de tirage pour déterminer l’effet de cette courbure. La prochaine publication présentera les calculs et l’analyse.
Dans la deuxième partie de cette série, nous examinons l’angle total de courbure par période P (répétition de pic à pic d’un tirage de câble). Nous expliquons comment l’angle de courbure par unité de longueur peut être utile pour effectuer les calculs sur la base de la nature répétitive de la période.